(本小题满分10分)学校足球队进行罚点球训练,队员在一轮训练中最多可罚4次,并规定,一旦命中该队员即停止此轮练习,否则一直罚到第4次为止. 已知一选手罚点球的命中率为0.8,求一轮练习中,该选手的实际罚球次数X的分布列,并求X的数学期望.
【选修4—4:坐标系与参数方程】(本小题满分10分)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.曲线C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为 (t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
【选修4—2:矩阵与变换】(本小题满分10分)
已知曲线 ,在矩阵M
,在矩阵M 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,
, 在矩阵N
在矩阵N 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,求曲线
,求曲线 的方程.
的方程.
【选修4—1几何证明选讲】(本小题满分10分)如图,在△ABC中,CM是∠ACB的平分线,△AMC的外接圆O交BC于点N. 若AB=2AC,
求证:BN=2AM.
(本小题满分16分)已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列 前n项和为
前n项和为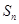 ,且满足
,且满足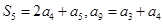 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若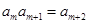 ,求正整数m的值;
,求正整数m的值;
(Ⅲ)是否存在正整数m,使得 恰好为数列
恰好为数列 中的一项?若存在,求出所有满足条件的m
中的一项?若存在,求出所有满足条件的m
值,若不存在,说明理由.