(本小题满分12分) 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在AB上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在AB上,且OM∥AC.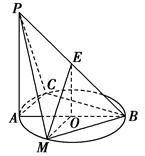
(1)求证:平面MOE∥平面PAC;
(2)求证:平面PAC⊥平面PCB;
(3)设二面角M-BP-C的大小为θ,求 的值.
的值.
已知直线 在矩阵 对应的变换作用下变为直线
(I)求实数
的值
(II)若点
在直线
上,且
,求点
的坐标
已知函数
的周期为
,图象的一个对称中心为
,将函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
单位长度后得到函数
的图象。
(Ⅰ)求函数
与
的解析式
(Ⅱ)是否存在
,使得
按照某种顺序成等差数列?若存在,请确定
的个数,若不存在,说明理由;
(Ⅲ)求实数
与正整数
,使得
在
内恰有2013个零点.
如图,在四棱柱 中,侧棱 底面 ,
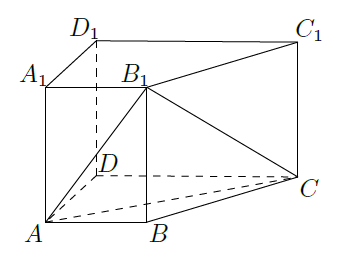
(Ⅰ)求证: 平面 .
(Ⅱ)若直线 与平面 所成角的正弦值为 ,求 的值.
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出 的解析式。(直接写出答案,不必说明理由).
如图,在正方形 中, 为坐标原点,点 的坐标为 ,点 的坐标为 ,分别将线段 和 十等分,分点分别记为 和 ,连接 ,过 作 轴的垂线与 交于点 。

(1)求证:点
都在同一条抛物线上,并求抛物线
的方程;
(2)过点
作直线
与抛物线E交于不同的两点
, 若
与
的面积之比为4:1,求直线
的方程。
已知函数 当 时,求曲线 在点 处的切线方程;求函数 的极值.