(本小题满分10分)【选修4—1:几何证明选讲】
在直角坐标系中,以原点为极点,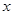 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线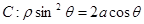
 ,已知过点
,已知过点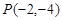 的直线
的直线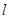 的参数方程为
的参数方程为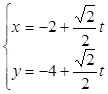 (
(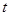 为参数),直线
为参数),直线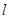 与曲线
与曲线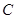 分别交于
分别交于 两点。
两点。
(1)写出曲线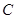 和直线
和直线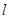 的普通方程;
的普通方程;
(2)若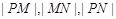 成等比数列,求
成等比数列,求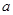 的值.
的值.
如图,已知矩形ABCD中,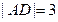 ,
,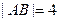 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.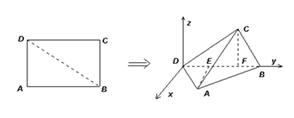
如图,长方体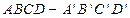 中,
中,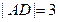 ,
,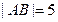 ,
,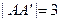 ,设E为
,设E为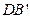 的中点,F为
的中点,F为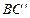 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,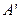 ,
,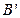 ,
,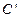 ,
,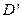 ,E,F各点的坐标.
,E,F各点的坐标.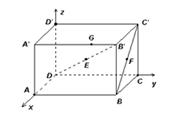
在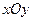 平面内的直线
平面内的直线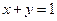 上确定一点
上确定一点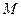 ;使
;使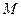 到点
到点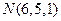 的距离最小.
的距离最小.
如下图,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(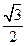 ,
, ,0),点D在平面yoz上,且
,0),点D在平面yoz上,且 BDC=900,
BDC=900, DCB=300,求点D的坐标。
DCB=300,求点D的坐标。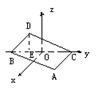
(1)写出点P(1,3,-5)关于原点成中心对称的点的坐标;
(2)写出点P(1,3,-5)关于ox轴对称的点的坐标。