已知椭圆 的离心率
的离心率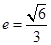 ,过点
,过点
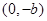 和
和
 的直线与原点的距离为
的直线与原点的距离为 .
. 
(1)求椭圆的方程;
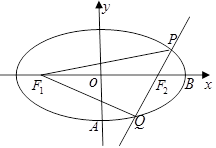
(2)设 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过 作直线交椭圆于
作直线交椭圆于 两点,求
两点,求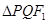 的内切圆半径
的内切圆半径 的最大值.
的最大值.
设 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上一点,若
是椭圆上一点,若 ,证明:
,证明: 的面积只与椭圆的短轴长有关
的面积只与椭圆的短轴长有关
从椭圆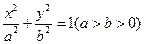 上一点
上一点 向
向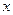 轴引垂线,垂足恰为椭圆的左焦点
轴引垂线,垂足恰为椭圆的左焦点 ,
, 为椭圆的右顶点,
为椭圆的右顶点, 是椭圆的上顶点,且
是椭圆的上顶点,且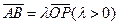 .
.
⑴求该椭圆的离心率.
⑵若该椭圆的准线方程是 ,求椭圆方程.
,求椭圆方程.
已知长方形ABCD, AB=2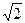 ,BC=1.以AB的中点
,BC=1.以AB的中点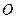 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系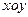 .
.
(Ⅰ)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(Ⅱ)过点P(0,2)的直线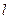 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线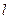 ,使得以弦MN为直径的圆恰好过原点?若存在,求出直线
,使得以弦MN为直径的圆恰好过原点?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.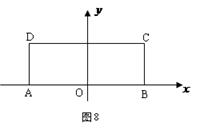
已知A、B分别是椭圆 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P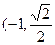 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。
(1)求椭圆的标准方程;
(2)点C是椭圆上异于长轴端点的任意一点,对于△ABC,求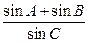 的值。
的值。
已知椭圆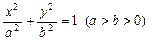 与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率
与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率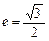 .求椭圆方程
.求椭圆方程