(本题满分14分)
某企业准备投资1200万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
| 学段 |
硬件建设(万元) |
配备教师数 |
教师年薪(万元) |
| 初中 |
26 / 班 |
2 / 班 |
2 / 人 |
| 高中 |
54 / 班 |
3 / 班 |
2 / 人 |
因生源和环境等因素,全校总班级至少20个班,至多30个班。
(Ⅰ)请用数学关系式表示上述的限制条件;(设开设初中班x个,高中班y个)
(Ⅱ)若每开设一个初、高中班,可分别获得年利润2万元、3万元,请你合理规划办学规模使年利润最大,最大为多少?
对于函数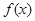 若存在
若存在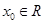 ,使得
,使得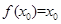 成立,则称
成立,则称 为
为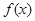 的不动点.
的不动点.
已知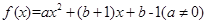
(1)当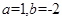 时,求函数
时,求函数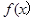 的不动点;
的不动点;
(2)若对任意实数 ,函数
,函数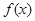 恒有两个相异的不动点,求
恒有两个相异的不动点,求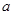 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上
图象上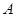 、
、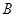 两点的横坐标是函数
两点的横坐标是函数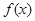 的不动点,且
的不动点,且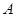 、
、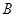 两点关于直线
两点关于直线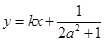 对称,求
对称,求 的最小值.
的最小值.
在平面直角坐标系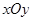 中,已知圆
中,已知圆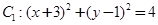 和圆
和圆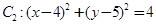 .
.
(1)若直线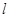 过点
过点 ,且被圆
,且被圆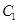 截得的弦长为
截得的弦长为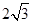 ,求直线
,求直线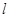 的方程;
的方程;
(2)设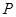 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点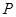 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线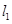 和
和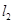 ,它们分别与圆
,它们分别与圆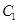 和圆
和圆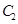 相交,且直线
相交,且直线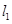 被圆
被圆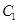 截得的弦长与直线
截得的弦长与直线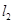 被圆
被圆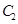 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点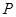 的坐标.
的坐标.
在三棱锥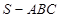 中,
中,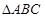 是边长为2的正三角形,平面
是边长为2的正三角形,平面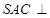 平面
平面 ,
,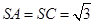 ,
, 分别为
分别为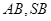 的中点.
的中点.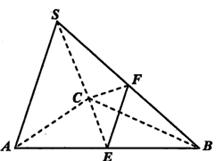
(1)证明: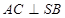 ;
;
(2)求锐二面角 的余弦值;
的余弦值;
已知函数
(1)求 的单调递增区间;
的单调递增区间;
(2)在 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为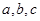 ,已知
,已知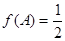 ,
, 成等差数列,且
成等差数列,且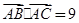 ,求边
,求边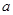 的值.
的值.
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.