相关部门对跳水运动员进行达标定级考核，动作自选，并规定完成动作成绩在八分及以上的定为达标，成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
（1）考核结束后，从参加考核的运动员中随机抽取了8人，发现这8人中有2人没有达标，有3人为一级运动员，据此请估计此次考核的达标率及被定为一级运动员的人数；
（2）经过考核，决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛（这五位运动员每位被选中的可能性相同）. 写出所有可能情况，并求运动员E被选中的概率.
计算：
（1）
；
（2）2lg5＋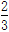
lg8＋lg5×lg20＋lg22．
某单位用2160万元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为x（x≥10）层，则每平方米的平均建筑费用为560＋48x（单位：元）．
（1）写出楼房平均综合费用y关于建造层数x的函数关系式；
（2）该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？
（注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用/建筑总面积）
已知数列{an}的前n项和为Sn，且向量a＝（n，Sn），b＝（4，n＋3）共线．
（1）求证：数列{an}是等差数列；
（2）求数列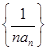
的前n项和Tn．
在△ABC中，a，b，c分别为内角A，B，C的对边，且2asin A＝（2b＋c）sin B＋（2c＋b）sin C．
（1）求A的大小；
（2）若sin B＋sin C＝1，试判断△ABC的形状．
已知等差数列{an}满足a2＝2，a5＝8．
（1）求{an}的通项公式；
（2）各项均为正数的等比数列{bn}中，b1＝1，b2＋b3＝a4，求{bn}的前n项和Tn．