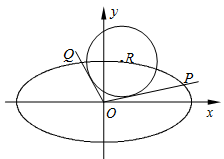
如图,在平面直角坐标系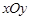 中,已知椭圆
中,已知椭圆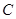 :
: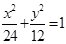 ,设
,设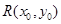 是椭圆
是椭圆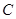 上的任一点,从原点
上的任一点,从原点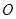 向圆
向圆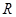 :
: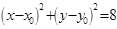 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点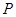 ,
,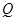 .
.
(1)若直线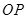 ,
,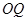 互相垂直,求圆
互相垂直,求圆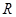 的方程;
的方程;
(2)若直线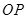 ,
,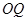 的斜率存在,并记为
的斜率存在,并记为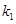 ,
,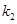 ,求证:
,求证: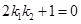 ;
;
(3)试问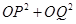 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| 文艺节目 |
新闻节目 |
总计 |
|
| 20至40岁 |
40 |
10 |
50 |
| 大于40岁 |
20 |
30 |
50 |
| 总计 |
60 |
40 |
100 |
(1)由表中数据检验,有没有99.9%把握认为收看文艺节目的观众与年龄有关?
(2)20至40岁,大于40岁中各抽取1名观众,求两人恰好都收看文艺节目的概率.
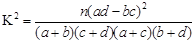
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
在 中,角
中,角 所对的边分别为
所对的边分别为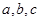 且满足
且满足
(I)求角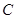 的大小;
的大小;
(II)求函数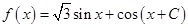
 的最大值,并求取得最大值时
的最大值,并求取得最大值时 的大小.
的大小.
(本小题满分15分)过曲线C: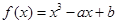 外的点A(1,0)作曲线C的切线恰有两条,
外的点A(1,0)作曲线C的切线恰有两条,
(Ⅰ)求 满足的等量关系;
满足的等量关系;
(Ⅱ)若存在 ,使
,使 成立,求
成立,求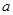 的取值范围.
的取值范围.
已知点 (0,1),
(0,1), ,直线
,直线 、
、 都是圆
都是圆 的切线(
的切线( 点不在
点不在 轴上).
轴上).
(Ⅰ)求过点 且焦点在
且焦点在 轴上的抛物线的标准方程;
轴上的抛物线的标准方程;
(Ⅱ)过点(1,0)作直线 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使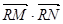 为常数?若存在,求出点
为常数?若存在,求出点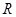 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为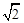 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.