已知函数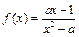 (1)当
(1)当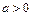 时,解关于
时,解关于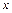 的不等式
的不等式
(2)若不等式 对
对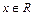 恒成立,求实数
恒成立,求实数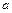 的值。
的值。
椭圆G: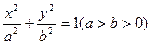 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足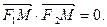
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为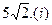 求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点
求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点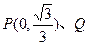 的直线对称?若能,求出k的取值范围;若不能,请说明理由
的直线对称?若能,求出k的取值范围;若不能,请说明理由
在平面直角坐标系xoy中,直线l与抛物线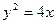 相交于不同的A、B两点.
相交于不同的A、B两点.
(Ⅰ)如果直线l过抛物线的焦点,求 的值;
的值;
(Ⅱ)如果 证明直线l必过一定点,并求出该定点
证明直线l必过一定点,并求出该定点
已知函数 ,设
,设 ,
,

(1)求 ,
, 的表达式,并猜想
的表达式,并猜想
 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于 的函数
的函数 在区间
在区间 上的最小值为6,求
上的最小值为6,求 的值
的值
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(Ⅰ)试解释 的实际意义;
的实际意义;
(Ⅱ)设 ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?