如图,在正三棱柱ABC—A1B1C1中,底面边长为 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且
 .
.
(1)求证: ;
;
(2)求四面体 的体积.
的体积.
已知函数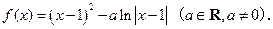
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间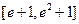 上的最小值.
上的最小值.
已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l的斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
正△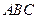 的边长为4,
的边长为4,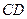 是
是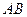 边上的高,
边上的高, 分别是
分别是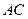 和
和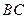 边的中点,现将△
边的中点,现将△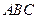 沿
沿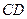 翻折成直二面角
翻折成直二面角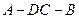 .
.
(1)试判断直线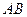 与平面
与平面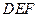 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角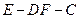 的余弦值;
的余弦值;
(3)在线段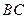 上是否存在一点
上是否存在一点 ,使
,使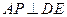 ?证明你的结论.
?证明你的结论.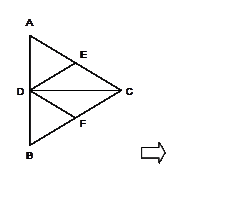

(12分)已知数列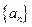 是各项均不为0的等差数列,
是各项均不为0的等差数列,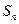 为其前
为其前 项和,且满足
项和,且满足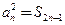 ,令
,令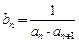 ,数列
,数列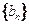 的前n项和为
的前n项和为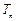 .
.
(Ⅰ)求数列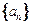 的通项公式及数列
的通项公式及数列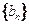 的前n项和
的前n项和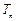 ;
;
(Ⅱ)是否存在正整数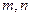
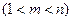 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的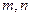 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(文)(本小题满分12分)
在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答对这道题的概率是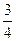 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是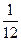 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是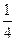 .
.
(1)求乙、丙两人各自回答对这道题的概率.
(2)求甲、乙、丙三人中恰有两人回答对该题的概率