(12分)已知数列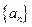 是各项均不为0的等差数列,
是各项均不为0的等差数列,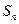 为其前
为其前 项和,且满足
项和,且满足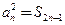 ,令
,令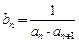 ,数列
,数列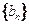 的前n项和为
的前n项和为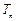 .
.
(Ⅰ)求数列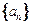 的通项公式及数列
的通项公式及数列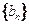 的前n项和
的前n项和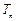 ;
;
(Ⅱ)是否存在正整数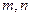
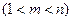 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的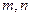 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间统计结果如下:
从第一个顾客开始办理业务时计时.
(1)估计第三个顾客恰好等待4分钟开始办理业务的概率;
(2)
表示至第2分钟末已办理完业务的顾客人数,求
的分布列及数学期望.
已知椭圆
,椭圆
以
的长轴为短轴,且与
有相同的离心率。
(1)求椭圆
的方程;
(2)设
为坐标原点,点
分别在椭圆
和
上,
,求直线
的方程.
(1)如图,证明命题"a是平面
内的一条直线,b是
外的一条直线(b不垂直于
),c是直线b在
上的投影,若
,则
"为真。
(2)写出上述命题的逆命题,并判断其真假(不需要证明)

设
的公比不为1的等比数列,其前
项和为
,且
成等差数列。
(1)求数列
的公比;(2)证明:对任意
,
成等差数列
函数
的最大值为3, 其图像相邻两条对称轴之间的距离为
.
(1)求函数
的解析式;
(2)设
,则
,求
的值