(本小题满分12分)在△ABC中,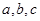 分别为内角
分别为内角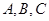 的对边,面积
的对边,面积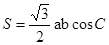 .
.
(1)求角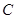 的大小;
的大小;
(2)设函数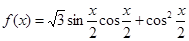 ,求
,求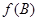 的最大值,及取得最大值时角
的最大值,及取得最大值时角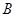 的值.
的值.
(1)已知数列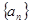 为等比数列,且
为等比数列,且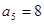 ,
,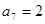 ,该数列的各项都为正数,求
,该数列的各项都为正数,求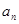 ;(2)若等比数列
;(2)若等比数列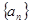 的首项
的首项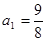 ,末项
,末项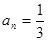 ,公比
,公比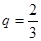 ,求项数
,求项数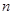 。
。
在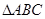 中,角A.、B、C的对边分别为
中,角A.、B、C的对边分别为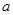 、
、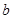 、
、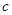 .角A.、B、C成等差数列。
.角A.、B、C成等差数列。
(1)求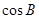 的值; (2)边
的值; (2)边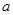 、
、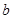 、
、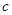 成等比数列,求
成等比数列,求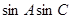 的值。
的值。
已知函数
(1)求函数 的单调区间;
的单调区间;
(2)若函数 对定义域内的任意的
对定义域内的任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设函数 ,且曲线
,且曲线 斜率最小的切线与直线
斜率最小的切线与直线 平行.求:(1)
平行.求:(1) 的值;(2)函数
的值;(2)函数 的单调区间.
的单调区间.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)回归分析,并求出y关于x的线性回归方程 =bx+a;
=bx+a;
(2)试预测加工10个零件需要多少时间?
| n-2 |
1 |
2 |
3 |
4 |
| 小概率0.05 |
0.997 |
0.950 |
0.878 |
0.811 |
| 小概率0.01 |
1.000 |
0.990 |
0.959 |
0.917 |