(本小题满分15分)学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 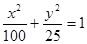 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为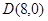 .观测点
.观测点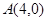 ,
, 同时跟踪航天器.
同时跟踪航天器.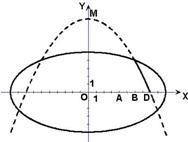
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2 km,甲10时出发前往乙家.如图所示,表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系.试写出y=f(x)的函数解析式.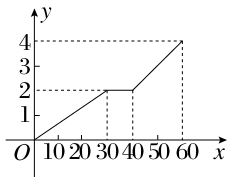
已知函数f(x)=x2-4ax+2a+6,x∈R.
(1)若函数的值域为[0,+∞),求a的值;
(2)若函数的值域为非负数集,求函数f(a)=2-a|a+3|的值域.
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p∨q”是假命题,求实数a的取值范围.
已知命题p:函数f(x)=x2+ax-2在[-1,1]内有且仅有一个零点.命题q:x2+3(a+1)x+2≤0在区间[ ,
, ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
已知命题P:函数y=loga(1-2x)在定义域上单调递增;命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若P∨Q是真命题,求实数a的取值范围.