(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=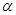 ,其中
,其中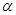 为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.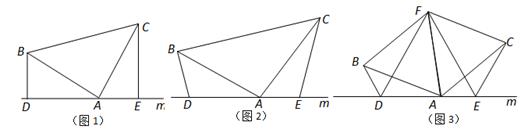
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图,已知反比例函数 的图象与直线 相交于点 , .
(1)求出直线 的表达式;
(2)在 轴上有一点 使得 的面积为18,求出点 的坐标.

如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼 的高度进行测量,先测得居民楼 与 之间的距离 为 ,后站在 点处测得居民楼 的顶端 的仰角为 ,居民楼 的顶端 的仰角为 ,已知居民楼 的高度为 ,小莹的观测点 距地面 .求居民楼 的高度(精确到 .(参考数据: , , .

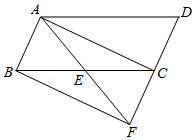
如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.
今年植树节期间,某景观园林公司购进一批成捆的 , 两种树苗,每捆 种树苗比每捆 种树苗多10棵,每捆 种树苗和每捆 种树苗的价格分别是630元和600元,而每棵 种树苗和每棵 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵, 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进 种树苗和 种树苗各多少棵?并求出最低费用.