某电视台拟举行由选手报名参加的比赛类型的娱乐节目，选手进入正赛前需通过海选，参加海选的选手可以参加A、B、C三个测试项目，只需通过一项测试即可停止测试，通过海选．若通过海选的人数超过预定正赛参赛人数，则优先考虑参加海选测试次数少的选手进入正赛．甲选手通过项目A、B、C测试的概率为分别为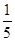
、
、
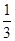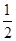， 且通过各次测试的事件相互独立．
（1）若甲选手先测试A项目，再测试B项目，后测试C项目，求他通过海选的概率；若改变测试顺序，对他通过海选的概率是否有影响？说明理由；
（2）若甲选手按某种顺序参加海选测试，第一项能通过的概率为p1，第二项能通过的概率为p2，第三项能通过的概率为p3，设他通过海选时参加测试的次数为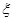
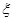，求的分布列和期望（用p1、p2、p3表示）；并说明甲选手按怎样的测试顺序更有利于他进入正赛．
（本小题满分14分）
已知
（Ⅰ）求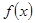
；
（Ⅱ）判断并证明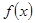的奇偶性与单调性;
（Ⅲ）若对任意的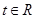
，不等式
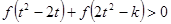恒成立，求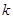
的取值范围。
（本小题满分12分）为了预防流感，某学校对教室用药熏消毒法进行消毒.已知药物释放过程中，室内每立方米空气的含药量
（毫克）与时间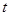
（小时）成正比.药物释放完毕后，与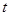的函数关系式为
（
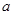为常数），如图所示，根据图中提供的信息，回答下列问题：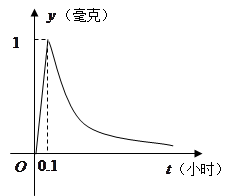
（1）求从药物释放开始，每立方米空气中的含药量（毫克）与时间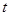（小时）之间的函数关系式；（2）据测定，当空气中每立方米空气的含药量降到0．25毫克以下时，学生方可进教室，那从药物释放开始，至少需要经过多少小时后，学生才能回到进教室？
（本小题满分12分）设函数
,
,
（Ⅰ）若
,求
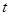取值范围;
（Ⅱ）求
的最值，并给出函数取最值时对应的x的值。
（本小题满分12分）已知集合
，
．
（Ⅰ） 若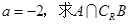
；
（Ⅱ） 若A∪B＝B，求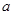
的取值范围。
（本小题满分12分）函数
是R上的偶函数，且当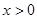
时，函数解析式为
,
（Ⅰ）求
的值；
（Ⅱ）求当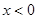
时，函数的解析式。