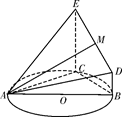
如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,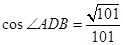 .
.
(1)求证:平面AEC⊥平面BCED;
(2)试问线段DE上是否存在点M,使得直线AM与平面ACE所成角的正弦值为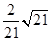 ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
| 数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
| 优秀 |
5 |
2 |
7 |
| 不优秀 |
1 |
12 |
13 |
| 合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到 “无效序号(序号大于20)”的概率.
参考公式: ,其中
,其中 )
)
临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数y=f(x)对任意的实数ab都有:f(a+b)=f(a)+f(b)﹣1,且x>0时,f(x)>1,
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,求f(2)的值,并解不等式f(3m2﹣m﹣2)<3.
已知f(x)=ax3+bx2+cx(a≠0)在x=1和x=-1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试求f(x) 的单调区间;
(3) 试判断x=±1时函数取极小值还是极大值,并说明理由.
已知某长方体的棱长之和为14.8m,长方体底面的一边比另一边长0.5m,问高为多少时长方体体积最大?并求出最大体积是多少?
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-mf(x)在[-1,1]上是增函数,求实数m的取值范围.