等比数列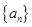 中的前三项a1、a2、a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
中的前三项a1、a2、a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
(1)求此数列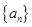 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本题满分15分)圆C过点A(2,0)及点B( ,
, ),且与直线l:y=
),且与直线l:y= 相切
相切
(1)求圆C的方程;
(2)过点P(2,1)作圆C的切线,切点为M,N,求|MN|;
(3)点Q为圆C上第二象限内一点,且∠BOQ= ,求Q点横坐标.
,求Q点横坐标.
(本题满分14分)△ABC中,已知角A、B、C的对边分别为a、b、c,若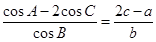 .
.
(1)求 的值;
的值;
(2)若b=2,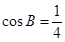 ,求△ABC的面积S.
,求△ABC的面积S.
(本题满分14分) 已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0}
(1)若A∩B=[1,3],求实数m的值;
(2)若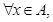 都有
都有 ,求实数m的取值范围.
,求实数m的取值范围.
如图,从椭圆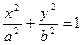
 上一点
上一点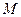 向
向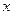 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点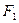 ,且它的长轴端点
,且它的长轴端点 及短轴端点
及短轴端点 的连线
的连线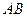 平行于
平行于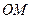 ,
,
(1)求椭圆的离心率;
(2)设 是椭圆上任意一点,
是椭圆上任意一点,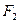 是右焦点,求
是右焦点,求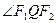 的取值范围;
的取值范围;
(3)设 是椭圆上一点,当
是椭圆上一点,当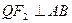 时,延长
时,延长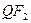 与椭圆交于另一点
与椭圆交于另一点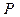 ,若
,若 的面积为
的面积为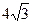 ,求此时的椭圆方程。
,求此时的椭圆方程。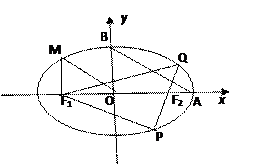
如图,在底面是矩形的四棱锥 中,
中, ,
, .
.
(1)求证:平面 ;
;
(2)若 为
为 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)在 上是否存在一点
上是否存在一点 ,使得
,使得 到平面
到平面 的距离为1?若存在,求出
的距离为1?若存在,求出 ,若不存在,请说明理由。
,若不存在,请说明理由。