(本小题满分12分) 某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取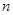
份试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在
，
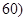的学生人数为6．
（Ⅰ）求直方图中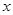
的值；
（Ⅱ）试估计所抽取的数学成绩的平均数；
（Ⅲ）试根据样本估计“该校高一学生期末数学考试成绩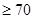
”的概率．
(本小题满分12分)
在△ABC中，已知
，c=1，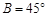
，求A ，C， a．
已知
是定义在
上的奇函数，当
时，
（1）求的解析式；
（2）是否存在负实数
，使得当
的最小值是4？如果存在，求出的值；如果不存在，请说明理由.
（3）对
如果函数
的图像在函数
的图像的下方，则称函数在D上被函数覆盖.求证：若
时，函数在区间
上被函数
覆盖.
为了保护环境，某工厂在政府部门的支持下，进行技术改进： 把二氧化碳转化为某种化工产品，经测算，该处理成本
（万元）与处理量
（吨）之间的函数关系可近似地表示为：
， 且每处理一吨二氧化碳可得价值为
万元的某种化工产品.
(Ⅰ)当
时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，则国家至少需要补贴多少万元，该工厂才不亏损？
（Ⅱ） 当处理量为多少吨时，每吨的平均处理成本最少.
（本小题12分） 已知二次函数
与
轴有两个交点
和
，若，且
.
（Ⅰ）求此二次函数的解析式
（Ⅱ）若
在闭区间
的最大值为
，求
的解析式及其最大值
(本小题满分12分）
设当
时，函数
的值域为
，且当
时，恒有
，求实数k的取值范围．