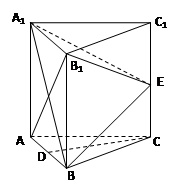(本小题满分13分)
对某校高三年级学生参加社区服务次数进行统计,随机抽取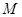 名学生作为样本,得到这
名学生作为样本,得到这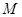 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中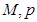 及图中
及图中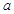 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间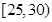 内的概率.
内的概率.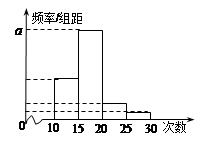
| 分组 |
频数 |
频率 |
 |
10 |
0.25 |
 |
24 |
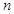 |
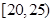 |
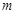 |
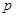 |
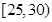 |
2 |
0.05 |
| 合计 |
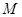 |
1 |
(本小题满分13分)在直角坐标系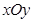 中,点P到两点
中,点P到两点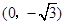 ,
,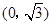 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为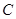 ,直线
,直线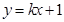 与C交于A,B两点.(1)写出C的方程;(2)若
与C交于A,B两点.(1)写出C的方程;(2)若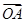
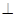
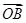 ,求k的值.
,求k的值.
(对于给定数列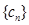 ,如果存在实常数
,如果存在实常数 ,使得
,使得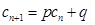 对于任意
对于任意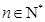 都成立,我们称数列
都成立,我们称数列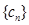 是 “M类数列”.
是 “M类数列”.
(I)若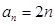 ,
,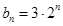 ,
,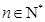 ,数列
,数列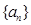 、
、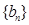 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数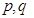 ,若不是,请说明理由;
,若不是,请说明理由;
(II)若数列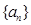 满足
满足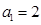 ,
,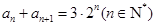 .
.
(1)求数列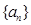 前
前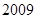 项的和.(2)已知数列
项的和.(2)已知数列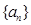 是 “M类数列”,求
是 “M类数列”,求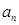 .
.
(已知,如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=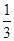 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为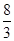 .(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
.(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求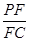 的值.
的值.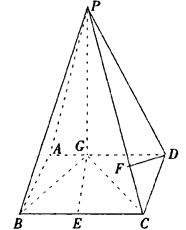
如图,在三棱柱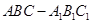 中,
中,
每个侧面均为正方形,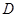 为底边
为底边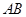 的中点,
的中点,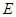 为侧棱
为侧棱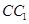 的中点.
的中点.
(Ⅰ)求证: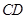 ∥平面
∥平面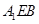 ;
;
(Ⅱ)求证: 平面
平面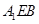 ;
;
(Ⅲ)求直线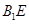 与平面
与平面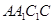 所成角的正弦值.
所成角的正弦值.