(本小题满分13分)
对某校高三年级学生参加社区服务次数进行统计,随机抽取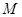 名学生作为样本,得到这
名学生作为样本,得到这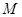 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中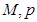 及图中
及图中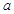 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间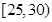 内的概率.
内的概率.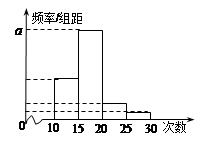
| 分组 |
频数 |
频率 |
 |
10 |
0.25 |
 |
24 |
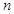 |
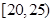 |
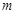 |
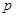 |
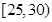 |
2 |
0.05 |
| 合计 |
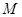 |
1 |
已知抛物线 y 2 =" –" x与直线 y =" k" ( x + 1 )相交于A、B两点, 点O是坐标原点.
(1) 求证: OA^OB;
(2) 当△OAB的面积等于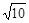 时, 求k的值.
时, 求k的值.
设椭圆C: 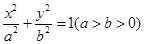 过点(0,4),离心率为
过点(0,4),离心率为 .
.
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为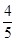 的直线被C所截得线段的中点坐标.
的直线被C所截得线段的中点坐标.
已知等差数列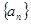 前
前 项和为
项和为 ,且
,且
(Ⅰ)求数列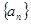 的通项公式;
的通项公式;
(Ⅱ)令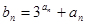 (
(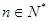 )求数列
)求数列 前
前 项和为
项和为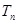
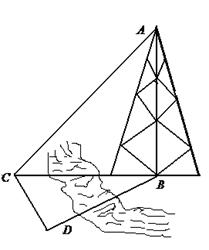
如图,测量河对岸的塔高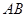 时,可以选与塔底
时,可以选与塔底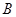 同一水平面内的两个测点
同一水平面内的两个测点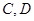 .现测得
.现测得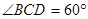 ,
, ,并在点
,并在点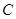 测得塔顶
测得塔顶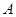 的仰角为
的仰角为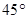 , 求塔高
, 求塔高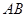 (精确到
(精确到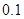 ,
,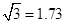 )
)
已知函数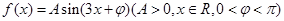 在
在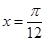 时取得最大值4.
时取得最大值4.
(1)求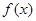 的最小正周期;
的最小正周期;
(2)求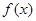 的解析式;
的解析式;
(3)若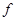 (
(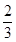 α+
α+ )=
)= ,求sinα.
,求sinα.