已知等比数列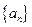 的首项为
的首项为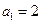 ,公比为
,公比为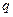 (
(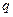 为正整数),且满足
为正整数),且满足 是
是 与
与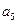 的等差中项;数列
的等差中项;数列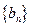 满足
满足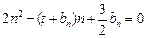 (
(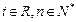 ).
).
(1)求数列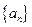 的通项公式;
的通项公式;
(2)试确定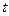 的值,使得数列
的值,使得数列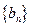 为等差数列;
为等差数列;
(3)当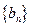 为等差数列时,对任意正整数
为等差数列时,对任意正整数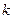 ,在
,在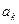 与
与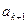 之间插入2共
之间插入2共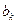 个,得到一个新数列
个,得到一个新数列 .设
.设 是数列
是数列 的前
的前 项和,试求满足
项和,试求满足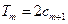 的所有正整数
的所有正整数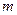 的值。
的值。
解关于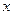 的不等式:
的不等式: .
. (12分)
(12分)
(本题10分)甲、乙两人各射击一次,击中目标的概率分别是 和
和 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间也没有影响.
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
(本题10分) 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整 数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
4 |
0.08 |
 60.5~70.5 60.5~70.5 |
0.16 |
|
| 70.5~80.5 |
10 |
|
| 80.5~90.5 |
16 |
0.32 |
| 90.5~100.5 |
||
| 合计 |
50 |

(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)
 补全频率分布直方图;
补全频率分布直方图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,
问该校获得二等奖的学生约为多少人?
在数列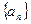 中,
中, ,
, ,令
,令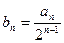 ,
,
(1)求 的值 (2)求
的值 (2)求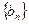 的前
的前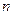 项和.(10分)
项和.(10分)
(本小题共14分)
已知数列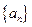 中,
中,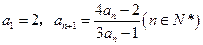 ,设
,设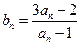 .
.
(Ⅰ)试写出数列 的前三项;
的前三项;
(Ⅱ)求证:数列 是等比数列,并求数列
是等比数列,并求数列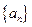 的通项公式
的通项公式 ;
;
(Ⅲ)设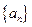 的前
的前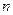 项和为
项和为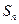 ,求证:
,求证: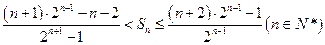 .
.