在直角坐标系xOy中,椭圆C1: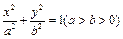 的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| =
的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| = 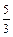 .
.
(1)求椭圆C1的方程;
(2)设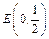 ,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
选做题(本小题满分10分。请考生三两题中任选一题做答,如果多做,
则按所做的第一题记分)
选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2。1)求DE的长;
(2)延长ED到P,过P作圆O的切线,
切点为C,若PC=2 ,求PD的长。
,求PD的长。
选修4-5:不等式选讲
(Ⅰ)若 与2的大小,不用说明理由;
与2的大小,不用说明理由;
(Ⅱ)设m是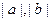 和1中最大的一个,当
和1中最大的一个,当

已知函数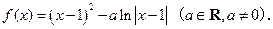
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间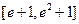 上的最小值.
上的最小值.
已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l的斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
正△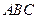 的边长为4,
的边长为4,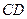 是
是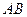 边上的高,
边上的高, 分别是
分别是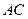 和
和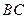 边的中点,现将△
边的中点,现将△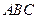 沿
沿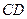 翻折成直二面角
翻折成直二面角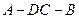 .
.
(1)试判断直线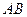 与平面
与平面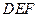 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角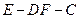 的余弦值;
的余弦值;
(3)在线段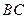 上是否存在一点
上是否存在一点 ,使
,使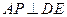 ?证明你的结论.
?证明你的结论.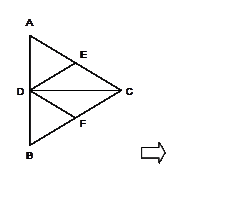

(12分)已知数列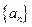 是各项均不为0的等差数列,
是各项均不为0的等差数列,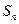 为其前
为其前 项和,且满足
项和,且满足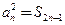 ,令
,令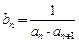 ,数列
,数列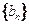 的前n项和为
的前n项和为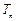 .
.
(Ⅰ)求数列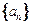 的通项公式及数列
的通项公式及数列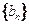 的前n项和
的前n项和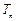 ;
;
(Ⅱ)是否存在正整数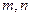
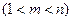 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的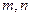 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.