如图,在等腰Rt△ABC中,∠ACB=90o,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE,连接DE、DF、EF。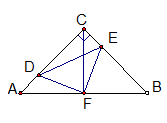
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
| 普通间(元/人/天) |
豪华间(元/人/天) |
贵宾间(元/人/天) |
|
| 三人间 |
50 |
100 |
500 |
| 双人间 |
70 |
150 |
800 |
| 单人间 |
100 |
200 |
1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: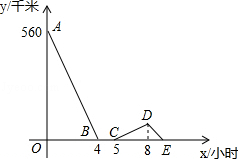
(1)甲乙两地之间的距离为千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
| 水银柱的长度x(cm) |
4.2 |
… |
8.2 |
9.8 |
| 体温计的读数y(℃) |
35.0 |
… |
40.0 |
42.0 |
(1)求y关于x的函数关系式;
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.
已知一次函数y=3x+m和y=-x+m的图象都经过点A(-2,3),且与x轴分别交于B、C两点,求△ABC的面积.
甲、乙两件服装的成本共500元,商店老板为获取利润,决定甲服装按50℅的利润标价,乙服装按40%的利润标价出售.在实际出售时,应顾客要求,两件服装均按标价的九折出售,这样商店共获利157元,求两件服装的成本各是多少元?