(本题10分)如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使 ,并写出点A2的坐标.
,并写出点A2的坐标.
(1)
(2)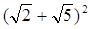
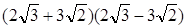
(4)
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r.则称P′为点P关于⊙C的反称点,下图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.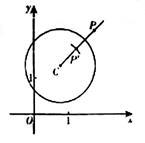
(1)当⊙O的半径为1时.
①分別判断点M(2,1),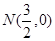 ,
,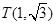 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=-x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x袖上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x袖上,半径为1,直线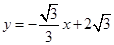 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
(.重庆市B卷,第26题,12分)如图,抛物线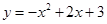 与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.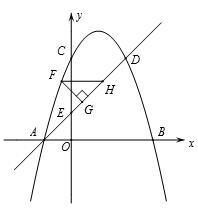
(1)求直线AD的解析式;
(2)如图,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.
(.重庆市A卷,第26题,12分)如图1,在平面直角坐标系中,抛物线 交
交 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与 轴的交点为D。
轴的交点为D。
图1
(1)求直线BC的解析式;
(2)点E(m,0),F(m+2,0)为 轴上两点,其中
轴上两点,其中 ,
, ,
, 分别垂直于
分别垂直于 轴,交抛物线与点
轴,交抛物线与点 ,
, ,交BC于点M,N,当
,交BC于点M,N,当 的值最大时,在
的值最大时,在 轴上找一点R,使
轴上找一点R,使 的值最大,请求出R点的坐标及
的值最大,请求出R点的坐标及 的最大值;
的最大值;
(3)如图2,已知 轴上一点
轴上一点 ,现以P为顶点,
,现以P为顶点, 为边长在
为边长在 轴上方作等边三角形QPG,使GP⊥
轴上方作等边三角形QPG,使GP⊥ 轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为
轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为 ,设
,设 与△ADC的重叠部分面积为s,当点
与△ADC的重叠部分面积为s,当点 到
到 轴的距离与点
轴的距离与点 到直线AW的距离相等时,求s的值。
到直线AW的距离相等时,求s的值。
|

(.河南省,第23题,11分)如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.
(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.
请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.