(.重庆市B卷,第26题,12分)如图,抛物线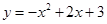 与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.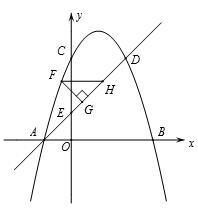
(1)求直线AD的解析式;
(2)如图,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.
已知抛物线 经过 , , 三点,对称轴是直线 .关于 的方程 有两个相等的实数根.
(1)求抛物线的解析式;
(2)若 ,试比较 与 的大小;
(3)若 , 两点在直线 的两侧,且 ,求 的取值范围.
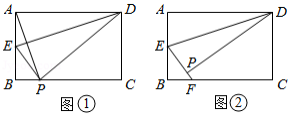
矩形 中, , .将矩形折叠,使点 落在点 处,折痕为 .
(1)如图①,若点 恰好在边 上,连接 ,求 的值;
(2)如图②,若 是 的中点, 的延长线交 于点 ,求 的长.
某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.

请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果;
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
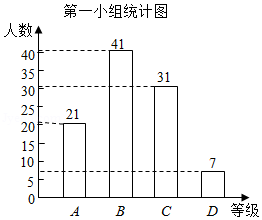
为了解全校学生对"垃圾分类"知识的掌握情况,某初级中学的两个兴趣小组分别抽样调查了100名学生.为方便制作统计图表,对"垃圾分类"知识的掌握情况分成四个等级: 表示"优秀", 表示"良好", 表示"合格", 表示"不合格".第一小组认为,八年级学生对"垃圾分类"知识的掌握不如九年级学生,但好于七年级学生,所以他们随机调查了100名八年级学生.
第二小组随机调查了全校三个年级中的100名学生,但只收集到90名学生的有效问卷调查表.
两个小组的调查结果如图的图表所示:
第二小组统计表
|
等级 |
人数 |
百分比 |
|
|
17 |
|
|
|
38 |
|
|
|
28 |
|
|
|
7 |
|
|
合计 |
90 |
|
若该校共有1000名学生,试根据以上信息解答下列问题:
(1)第 小组的调查结果比较合理,用这个结果估计该校学生对"垃圾分类"知识掌握情况达到合格以上(含合格)的共约 人;
(2)对这两个小组的调查统计方法各提一条改进建议.
如图,直线 与过点 的直线 交于点 ,与 轴交于点 .
(1)求直线 的解析式;
(2)点 在直线 上, 轴,交直线 于点 ,若 ,求点 的坐标.
