AB两地间铺有通讯电缆,它是由两条并在一起彼此绝缘的均匀导线组成,通常称为双线电缆。电缆长为L,每一条电缆的电阻为R.某次事故中不小心损坏了电缆,电缆的损坏有两种可能情况:绝缘层轻微受损,导致两导线间漏电,简称漏电故障(相当于在该处的两导线间接有一个电阻);绝缘层严重破坏,导致两导线直接短路,称之为短路故障。设导线间只有一处绝缘层破损。为判断破损处是哪种情况,在AB两端均处开路的前提下做了以下工作:
(1)在A地两端间接一恒压电源U,在B地两端间接理想电压表,测出电压表示数为UB ,在B地两端间接同一电源,在A地两端间接理想电压表,测出电压表示数为UA .若UA = UB =0,是什么故障类型?若UA ≠0,UB ≠0,是什么故障类型?
(2)在A地两端间接欧姆表测出电阻为RA,在B地两端间接欧姆表测出电阻为RB。
若RA+RB ="2R" ,请判断故障类型,并求出故障处与A、B端的距离之比。
若RA+RB >2R ,请判断故障类型,并求出故障处与A、B端的距离之比。
水平面上有电阻不计的U形导轨NMPQ,它们之间的宽度为L,M和P之间接入电动势为E的电源(不计内阻)。现垂直于导轨搁一根质量为m,电阻为R的金属棒ab,并加一个范围较大的匀强磁场,磁感应强度大小为B,方向与水平面夹角为θ且指向右斜上方,如图所示,问: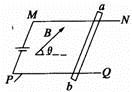
(1)当ab棒静止时,受到的支持力和摩擦力各为多少?
(2)若B的大小和方向均能改变,则要使ab棒所受支持力为零, B的大小至少为多少?此时B的方向如何?
如图甲所示,电荷量为q=1×10-4C的带正电的小物块置于粗糙绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动速度与时间t的关系如图丙所示,取重力加速度g=10m/s2。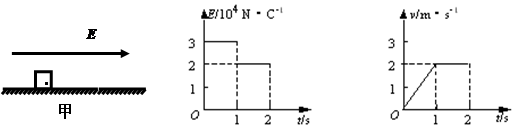
求:(1)前2秒内电场力做的功;
(2)物块的质量。
8月中旬,代号“突击-2013”的陆军航空兵实兵演习在粤东某海域举行.图为轰炸机在海平面上空进行投弹训练的示意图,轰炸机沿水平方向做匀加速直线运动.当轰炸机飞经观察点B点正上方A点时投放第一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时轰炸机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求:
⑴轰炸机投弹时离地面的高度h;
⑵第一颗炸弹落在C点时速度的大小;
⑶两次投弹时间间隔T内飞机飞行距离大小.
如图所示,质量为m= kg的小球置于倾角为30°的光滑固定斜面上,劲度系数为k=200N/m的轻弹簧一端系在小球上,另一端固定在P点,小球静止时,弹簧与竖直方向的夹角为30°.取g=10m/s2.求:
kg的小球置于倾角为30°的光滑固定斜面上,劲度系数为k=200N/m的轻弹簧一端系在小球上,另一端固定在P点,小球静止时,弹簧与竖直方向的夹角为30°.取g=10m/s2.求:
⑴小球对斜面的压力的大小;
⑵弹簧的伸长量;
⑶弹簧被剪断的瞬间,小球的加速度.
一物体在水平推力F=15N的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图象如图所示.g取10m/s2,求: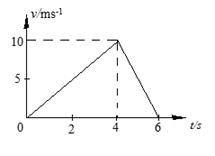
⑴ 0~4s和4~6s物体的加速度大小;
⑵物体与水平面间的动摩擦因数μ和物体的质量m;
⑶在0~6s内物体运动平均速度的大小.