2014年11月10日APEC会议在北京召开,某服务部需从大学生中招收志愿者,被招收的志愿者需参加分笔试和面试两部分,把参加笔试的 40 名大学生的成绩分组: 第 1 组[75,80),第 2 组 [80,85),第 3 组[85, 90),第 4 组 [90, 95),第 5 组[95,100),得到频率分布直方图如图所示: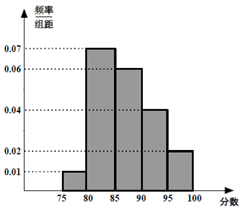
(Ⅰ)分别求成绩在第 4,5 组的人数;
(Ⅱ)现决定在笔试成绩较高的第 3,4,5 组中用分层抽样抽取 6 名进入面试,
①已知甲和乙的成绩均在第 3 组,求甲和乙同时进入面试的概率;
②若从这 6 名学生中随机抽取 2 名学生接受考官 D 的面试,设第 4 组中有 X 名学生被考官 D 面试,求X的分布列和数学期望.
(本小题满分12分)在举办的环境保护知识有奖问答比赛中,甲、乙、丙同时回答一道有关环境保护知识的问题,已知甲回答对这道题目的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.
(1)求乙、丙两人各自回答对这道题目的概率.
(2)求甲、乙、丙三人中至少有两人回答对这道题目的概率.
(本小题满分12分)如图,四棱锥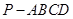 中,底面
中,底面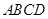 为矩形,
为矩形,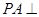 底面
底面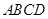 ,
,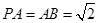 ,点
,点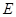 是棱
是棱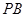 的中点.
的中点.
(1)证明: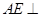 平面
平面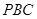 ;
;
(2)若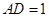 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 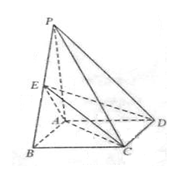
在数列 中,
中,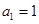 ,
,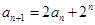 .
.
(1)设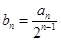 ,证明:数列
,证明:数列 是等差数列;
是等差数列;
(2)求数列 的前
的前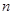 项和
项和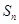 .
.
(本小题满分10分)
在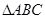 中,角
中,角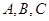 所对的边分别为
所对的边分别为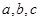 ,且满足
,且满足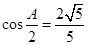 ,
, 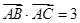 .
.
(1)求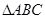 的面积;(2)若
的面积;(2)若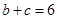 ,求
,求 的值.
的值.
已知函数 .
.
(Ⅰ)若函数在区间 上存在极值(
上存在极值(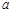 >0),求实数
>0),求实数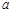 的取值范围;
的取值范围;
(Ⅱ)如果当 ,不等式
,不等式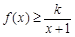 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(Ⅲ)求证: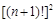 >
>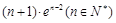 .
.