(本小题满分10分)
在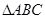 中,角
中,角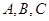 所对的边分别为
所对的边分别为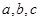 ,且满足
,且满足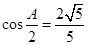 ,
, 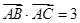 .
.
(1)求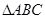 的面积; (2)若
的面积; (2)若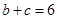 ,求
,求 的值.
的值.
(本小题满分12分)
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间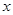 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率 之间的关系:
之间的关系:
时间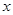 |
1 |
2 |
3 |
4 |
5 |
命中率 |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
求小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程 中系数计算公式
中系数计算公式 ,
, ,
,
.已知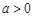 ,函数
,函数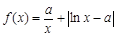 ,
,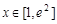 .
.
(Ⅰ)当 时,求曲线
时,求曲线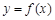 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若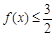 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,分别过椭圆E: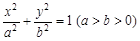 左右焦点
左右焦点 、
、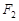 的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率
的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率 、
、 、
、 、
、 满足
满足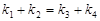 .已知当l1与x轴重合时,
.已知当l1与x轴重合时, ,
,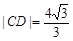 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在定点M、N,使得 为定值.若存在,求出M、N点坐标,若不存在,说明理由.
为定值.若存在,求出M、N点坐标,若不存在,说明理由.
如图,四边形ABCD中, 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在 内.
内.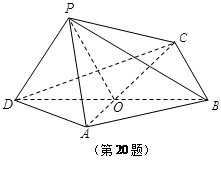
(Ⅰ)求证: 平面PBD;
平面PBD;
(Ⅱ)若已知二面角 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小.
数列 是公比为
是公比为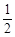 的等比数列,且
的等比数列,且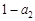 是
是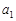 与
与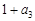 的等比中项,前
的等比中项,前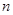 项和为
项和为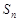 .数列
.数列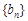 是等差数列,
是等差数列,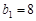 ,前
,前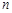 项和
项和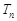 满足
满足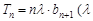 为常数,且
为常数,且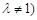 .
.
(Ⅰ)求数列 的通项公式及
的通项公式及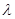 的值;
的值;
(Ⅱ)比较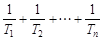 与
与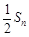 的大小.
的大小.