如图，分别过椭圆E：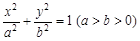
左右焦点
、
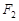的动直线l1、l2相交于P点，与椭圆E分别交于A、B与C、D不同四点，直线OA、OB、OC、OD的斜率
、
、
、
满足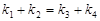
．已知当l1与x轴重合时，
，
．
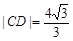（Ⅰ）求椭圆E的方程；
（Ⅱ）是否存在定点M、N，使得
为定值．若存在，求出M、N点坐标，若不存在，说明理由．
解关于
的不等式
如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=
．
（Ⅰ）证明：平面A1BD∥平面CD1B1；
（Ⅱ）求三棱柱ABD﹣A1B1D1的体积．
已知正方形ABCD的边长是13，平面ABCD外一点P到正方形各顶点的距离都为13，M、N分别是PA、BD上的点且PM：MA=BN：ND=5：8，如图．
（1）求证：直线MN∥平面PBC；
（2）求线段MN的长．
一盒中装有各色球12只，其中5个红球，4个黑球，2个白球，1个绿球；从中随机取出1球．求：
（1）取出的1球是红球或黑球的概率；
（2）取出的1球是红球或黑球或白球的概率．
如图所示，四边形ABCD是矩形，P∉平面ABCD，过BC作平面BCFE交AP于E，交DP于F．
求证：四边形BCFE是梯形．