已知函数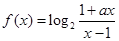 (a为常数)是奇函数.
(a为常数)是奇函数.
(Ⅰ)求a的值与函数 的定义域;
的定义域;
(Ⅱ)若当 时,
时,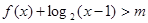 恒成立.求实数
恒成立.求实数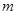 的取值范围.
的取值范围.
(本小题满分14分) 
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
(Ⅰ)将y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
(本小题满分14分)
设函数 有两个极值点
有两个极值点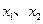 ,且
,且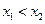
(I)求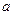 的取值范围,并讨论
的取值范围,并讨论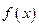 的单调性;
的单调性;
(II)证明: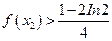
(本小题满分14分)如图,两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧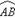 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为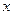 km,建在C处的垃圾处理厂对城A和城B的总影响度为
km,建在C处的垃圾处理厂对城A和城B的总影响度为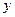 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在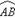 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.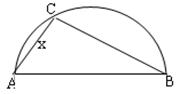
(I)将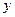 表示成
表示成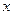 的函数;
的函数;
(II)讨论(1)中函数的单调性,并判断弧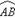 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(本小题满分14分)已知椭圆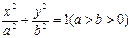 的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=
的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=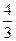 , |PF2|=
, |PF2|=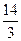 .
.
(I)求椭圆C的方程;
(II)若直线L过圆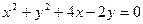 的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
(本小题满分14分)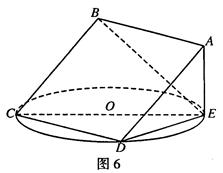
如图6,正方形ABCD所在平面与圆O所在平面
相交于CD,线段CD为圆O的弦,AE垂直于圆
O所在平面,垂足E是圆O上异于C、D的点,
AE=3,圆O的直径为9.
(1)求证:平面 ABCD ⊥平面 ADE;
(2)求二面角D—BC—E的平面角的正切值.