(本小题满分12分)甲、乙两名射击运动员参加某项有奖射击活动(射击次数相同).已知两名运动员射击的环数都稳定在7,8,9,10环,他们射击成绩的条形图如下: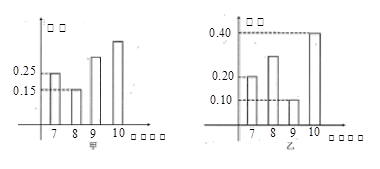
(Ⅰ)求乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率.
(Ⅱ)甲、乙两名运动员现在要同时射击4次,如果甲、乙同时击中9环以上(包括9环)3次时,可获得总奖金两万元;如果甲、乙同时击中9环以上(包括9环)4次时,可获得总奖金五万元,其他结果不予奖励.求甲、乙两名运动员可获得总奖金数的期望值.
(注:频率可近似看作概率)
设 ,圆
,圆 :
: 与
与 轴正半轴的交点为
轴正半轴的交点为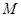 ,与曲线
,与曲线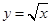 的交点为
的交点为 ,直线
,直线 与
与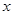 轴的交点为
轴的交点为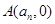 .
.
(1)求证: ;
;
(2)设 ,
,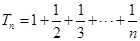 ,求证:
,求证: .
.
设函数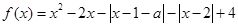
(1)当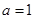 时,求
时,求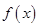 的最小值;
的最小值;
(2)对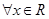 ,
,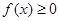 恒成立,求
恒成立,求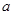 的取值范围.
的取值范围.
设椭圆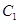 :
: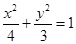 ,
,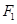 ,
,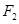 分别是椭圆的左右焦点,过椭圆右焦点
分别是椭圆的左右焦点,过椭圆右焦点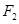 的直线
的直线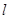 与椭圆
与椭圆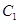 交于
交于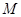 ,
,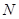 两点.
两点.
(1)是否存在直线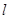 ,使得
,使得 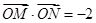 ,若存在,求出直线
,若存在,求出直线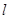 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(2)若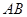 是椭圆
是椭圆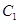 经过原点
经过原点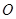 的弦,且
的弦,且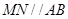 ,求证:
,求证: 为定值.
为定值.
如图,四棱锥 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,
是菱形, ,点
,点 在底面
在底面 上的射影为
上的射影为 的重心,点
的重心,点 为线段
为线段 上的点.
上的点.
(1)当点 为
为 的中点时,求证:
的中点时,求证: 平面
平面 ;
;
(2)当平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求
时,求 的值.
的值.
在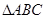 中,角
中,角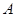 ,
,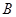 ,
,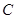 所对的边分别为
所对的边分别为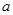 ,
,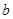 ,
,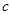 ,已知
,已知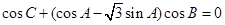
(1)求角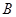 的大小;
的大小;
(2)若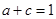 ,求
,求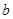 的取值范围.
的取值范围.