(本小题满分12分)甲、乙、丙三位同学彼此独立地从A、B、C、D、E五所高校中,任选2所高校参加自主招生考试(并且只能选2所高校),但同学甲特别喜欢A高校,他除选A校外,在B、C、D、E中再随机选1所;同学乙和丙对5所高校没有偏爱,都在5所高校中随机选2所即可.
(1)求甲同学未选中E高校且乙、丙都选中E高校的概率;
(2)记X为甲、乙、丙三名同学中未参加E校自主招生考试的人数,求X的分布列及数学期望.
已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(1)求通项公式an;
(2)设bn=2an,求数列{bn}的前n项和Sn.
△ABC中内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B.
(1)求B;
(2)若b=2,求△ABC面积的最大值.
如图,在△ABC中,∠ABC=90°,AB=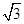 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.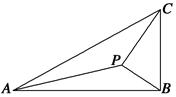
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
已知函数f(x)=2cos (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈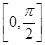 ,f
,f =-
=-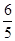 ,f
,f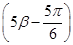 =
=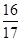 ,求cos(α+β)的值.
,求cos(α+β)的值.
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 |
甲 |
乙 |
|||
| 首次出现故 障时间x(年) |
0<x≤1 |
1<x≤2 |
x>2 |
0<x≤2 |
x>2 |
| 轿车数量(辆) |
2 |
3 |
45 |
5 |
45 |
| 每辆利润 (万元) |
1 |
2 |
3 |
1.8 |
2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.