旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率;
(2)求恰有2条线路没有被选择的概率;
(3)设选择甲线路旅游团的个数为 ,求
,求 的分布列
的分布列
| ξ |
0 |
1 |
2 |
3 |
| P |
 |
 |
 |
 |
(本小题满分12分)已知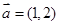 ,
, ,当
,当 为何值时,
为何值时,
(1) 与
与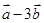 垂直?
垂直?
(2)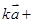
 与
与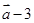
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(本小题满分12分)已知函数 的定义域为集合
的定义域为集合 ,
, 的值域为集合
的值域为集合 ,
, .
.
(1)求 和
和 ; (2)求
; (2)求 、
、 .
.
(本题13分)已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
(1)证明数列 是等比数列;
是等比数列;
(2)设 ,求
,求 ;
;
(3)记 ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1
(本题13分)如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值 ,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积
,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积 与种花的面积
与种花的面积 的比值
的比值 称为“草花比y”。
称为“草花比y”。
(1)设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
(2)当BE为多长时, 有最小值?最小值是多少?
有最小值?最小值是多少?
(本题12分)求过两直线 和
和 的交点且与直线
的交点且与直线 垂直的直线方程。
垂直的直线方程。