已知矩阵M = ,N =
,N =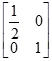 ,试求曲线
,试求曲线 在矩阵MN变换下的函数解析式.
在矩阵MN变换下的函数解析式.
记函数 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(Ⅰ)求集合 ;
;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
选修 :不等式选讲
:不等式选讲
已知函数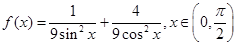 ,且
,且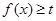 恒成立.
恒成立.
(Ⅰ)求实数 的最大值;
的最大值;
(Ⅱ)当 取最大值时,求不等式
取最大值时,求不等式 的解集.
的解集.
选修 ;坐标系与参数方程
;坐标系与参数方程
在直角坐标系 中,直线
中,直线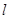 的参数方程为
的参数方程为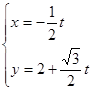 (
(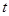 为参数),若以原点
为参数),若以原点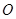 为极点,
为极点, 轴正半轴为极轴建立极坐标系,已知圆
轴正半轴为极轴建立极坐标系,已知圆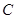 的极坐标方程为
的极坐标方程为 ,设
,设 是圆
是圆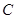 上任一点,连结
上任一点,连结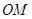 并延长到
并延长到 ,使
,使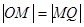 .
.
(Ⅰ)求点 轨迹的直角坐标方程;
轨迹的直角坐标方程;
(Ⅱ)若直线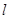 与点
与点 轨迹相交于
轨迹相交于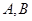 两点,点
两点,点 的直角坐标为
的直角坐标为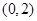 ,求
,求 的值.
的值.
选修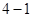 :几何证明选讲
:几何证明选讲
如图,圆内接四边形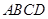 的边
的边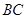 与
与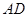 的延长线交于点
的延长线交于点 ,点
,点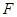 在
在 的延长线上.
的延长线上.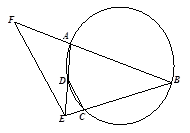
(Ⅰ)若 ,求
,求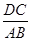 的值;
的值;
(Ⅱ)若 ,证明:
,证明: .
.
已知函数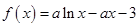 (
(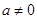 ).
).
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)若 对任意
对任意 恒成立,求实数
恒成立,求实数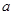 的取值范围(
的取值范围(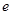 为自然常数);
为自然常数);
(Ⅲ)求证: (
( ,
, ).
).