(本小题满分12分)甲乙两支球队进行总决赛,比赛采用五场三胜制,即若有一队先胜三场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一,据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(Ⅰ)求总决赛中获得门票总收入恰好为220万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为X,求X的分布列和数学期望 .
.
(本小题满分12分)已知函数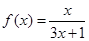 ,数列
,数列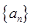 满足
满足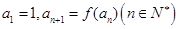 .
.
(1)求数列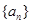 的通项公式;
的通项公式;
(2)记 ,证明:
,证明: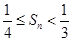 .
.
(本小题满分12分)如图,平面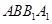 为圆柱
为圆柱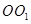 的轴截面,点
的轴截面,点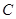 为底面圆周上异于
为底面圆周上异于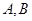 的任意一点.
的任意一点.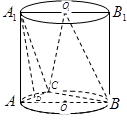
(1)求证: 平面
平面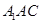 ;
;
(2)若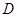 为
为 的中点,求证:
的中点,求证: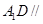 平面
平面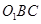 .
.
(本小题满分12分)某校高三文科(1)班学生参加“大联考”,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布区间为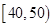 ,
,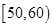 ,
,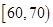 ,
,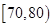 ,
,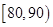 ,
,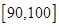 ,现已知成绩落在
,现已知成绩落在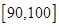 的有
的有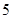 人.
人.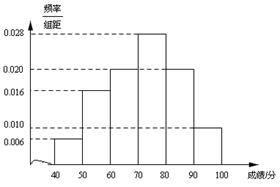
(1)求该校高三文科(1)班参加“大联考”的总人数;
(2)根据频率分布直方图,估计该班此次数学成绩的平均分(可用中值代替各组数据的平均值);
(3)现要从成绩在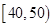 和
和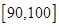 的学生中共选
的学生中共选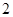 人参加某项座谈会,求
人参加某项座谈会,求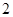 人来自于同一分数段的概
人来自于同一分数段的概
率.
(本小题满分12分)设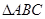 的内角
的内角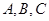 所对边的长分别是
所对边的长分别是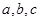 ,且
,且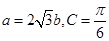 .
.
(1)求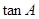 的值;
的值;
(2)若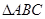 的面积为
的面积为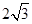 ,求
,求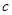 的值.
的值.
(本小题满分14分)已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数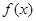 的单调区间;
的单调区间;
(Ⅱ)若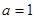 ,
,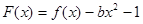 的导数
的导数 在
在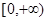 上是增函数,求实数b的最大值;
上是增函数,求实数b的最大值;
(Ⅲ)求证: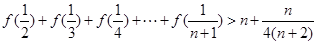 对一切正整数
对一切正整数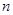 均成立.
均成立.