(本题14分)已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.
(1)问多少秒后,甲到A,B,C的距离和为40个单位?
(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?
(3)在(1)(2)的条件下,当甲到A、B、C的距离和为40个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
(本题满分12分)
已知点C为线段AB上一点, 分别以AC、BC为边在线段AB同侧作△ACD和△BCE, 且CA=CD, CB=CE, ∠ACD=∠BCE, 直线AE与BD交于点F.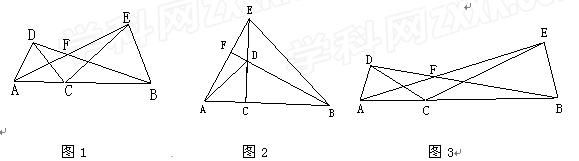
(1)如图1,求证:△ACE≌△DCB。
(2)如图1, 若∠ACD=60°, 则∠AFB= ;
如图2, 若∠ACD=90°, 则∠AFB= ;
(3)如图3, 若∠ACD=β, 则∠AFB= (用含β的式子表示)
并说明理由。
(本题满分9分)
在平行四边形 OABC中,已知A、C两点坐标分别为A(
OABC中,已知A、C两点坐标分别为A(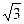 ,-
,-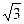 ),C(2
),C(2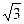 ,0)。
,0)。
(1)求B点的坐标
(2)将平行四边形OABC向左平移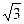 个单位长度,求所得平行四边形O′A′B′C′的四个顶点的坐标。
个单位长度,求所得平行四边形O′A′B′C′的四个顶点的坐标。
(3)求平行四边形OABC的面积。
(本题满分7分)
如图,在△ABC中,AB=AC,D为BC上一点 ,且AB=BD,AD=DC,求∠BAC的度数。
,且AB=BD,AD=DC,求∠BAC的度数。
如图所示,已 知点A、B、C、D在同一条直线上,AM=CN,BM=DN,∠M=∠N,求证:AC=BD
知点A、B、C、D在同一条直线上,AM=CN,BM=DN,∠M=∠N,求证:AC=BD 。
。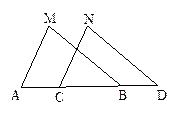
(本题满分5分)
有两条河流交汇形成一个三角地带,此地域风景宜人,土壤肥沃,小猪想择此地建造房屋P,他想到两条河流距离要相等,并且与两河交汇点的距离需200米。小猪不知道该怎么选择,你能帮助他吗?
(尺规作图,保留作图痕迹)