新学期，两摞规格相同的数学课本整齐的叠放在课桌上，请根据图中所给出的数据信息，解答下列问题： 
（1）每本书的厚度为 cm，课桌的高度为 cm；（每空2分，共4分）
（2）当课本数为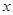
（本）时，请直接写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含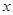的代数式表示）；
（3）利用（2）中的结论解决问题：桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本高出地面的距离．
如图，在平面直角坐标系中，已知点A坐标为（2，4），直线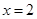
与
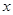轴相交于点B，连结OA，抛物线
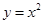从点O沿OA方向平移，与直线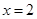交于点P，顶点M到A点时停止移动．
（1）求线段OA所在直线的函数解析式；
（2）设抛物线顶点M的横坐标为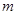
,①用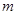的代数式表示点P的坐标；②当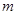为何值时，线段PB最短；
（3）当线段PB最短时，相应的抛物线上是否存在异于M的点Q，使△PQA的面积与△PMA的面积相等，若存在，请求出点Q的坐标；若不存在，请说明理由．
已知：关于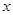
的—次函数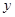
＝
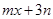和反比例函数＝
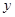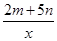的图象都经过点（1，－2）．求：
（1）—次函数和反比例函数的解析式；
（2）两个函数图象的另一个交点的坐标；
（3）请你直接写出不等式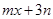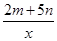＞的解集．
小张骑车往返于甲、乙两地，距甲地的路程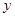
（千米）与时间
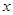（小时）的函数图象如图所示．
（1）小张在路上停留小时，他从乙地返回时骑车的速度为千米／时．
（2）小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止，途中小李与小张共相遇3次．请在图中画出小李距甲地的路程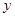（千米）与时间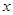（小时）的函数的大致图象．
（3）小王与小张同时出发，按相同路线前往乙地，距甲地的路程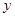（千米）与时间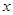（小时）的函数关系式为
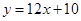．小王与小张在途中共相遇次？请你计算第一次相遇的时间．
已知一次函数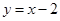
过抛物线
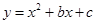与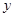
轴的交点及抛物线的顶点，求二次函数的解析式.
已知二次函数当
时，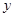
有最大值为5，且它的图象经过点（2，3），求：
（1）这个函数的关系式；
（2）当函数值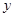不小于3时，请直接写出对应的自变量
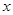的取值范围.