已知抛物线抛物线y n=-（x-an）2+an（n为正整数，且0<a1<a2<…<an）与x轴的交点为An-1（bn-1,0）和An（bn，0），当n=1时，第1条抛物线y1=-（x-a1）2+a1与x轴的交点为A0（0，0）和A1（b1，0），其他依此类推．
（1）求a1,b1的值及抛物线y2的解析式；
（2）抛物线y3的顶点坐标为（ ， ）；
依此类推第n条抛物线yn的顶点坐标为（ ， ）;
所有抛物线的顶点坐标满足的函数关系是 ；
（3）探究下列结论：
若用An-1An表示第n条抛物线被x轴截得得线段长，直接写出A0A1的值，并求出An-1An；
如图，在△ABC中，点D为BC边的中点，以点D为顶点的∠EDF的两边分别与边AB，AC交于点E，F，且∠EDF与∠A互补．
（1）如图1，若AB=AC，且∠A=90°，则线段DE与DF有何数量关系？请直接写出结论；
（2）如图2，若AB=AC，那么（1）中的结论是否还成立？若成立，请给出证明；若不成立，请说明理由；
（3）如图3，若AB：AC=m：n，探索线段DE与DF的数量关系，并证明你的结论．
如图，AB是⊙O的直径，点C在⊙O上，CD与⊙O相切， AD∥BC，连结OD，AC．
（1）求证：∠B=∠DCA；
（2）若tan B=
，OD=
， 求⊙O的半径长．
阅读下列材料：小华遇到这样一个问题：已知：如图1，在△ABC中，AB=
，AC=
，BC=2三边的长分别为，求∠A的正切值．
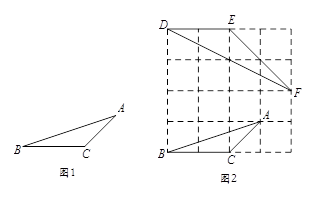
小华是这样解决问题的：如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．
（1）图2中与
相等的角为， 的正切值为；
（2）参考小华解决问题的方法，利用图4中的正方形网格（每个小正方形的边长均为1）解决问题：如图3，在△GHK中，HK=2，HG=
，KG=
，延长HK，求
的度数． 
如图，⊙O的直径CD与弦AB垂直相交于点E，且BC=1，AD=2，求⊙P的直径长.
下表给出了代数式
与
的一些对应值：
|
…… |
-2 |
-1 |
0 |
1 |
2 |
3 |
…… |
 |
…… |
5 |
 |
c |
2 |
-3 |
-10 |
…… |
（1）根据表格中的数据，确定
，
，的值；
（2）设
，直接写出
时
的最大值．