小明在解一元二次方程时,发现有这样一种解法:
如:解方程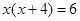 .
.
解:原方程可变形,得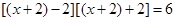 .
.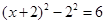 ,
,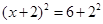 ,
,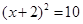 .
.
直接开平方并整理,得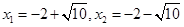 .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程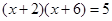 时写的解题过程.
时写的解题过程.
解:原方程可变形,得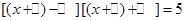 .
.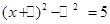 ,
,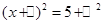 .
.
直接开平方并整理,得 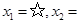 ¤.
¤.
上述过程中的“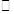 ”,“
”,“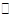 ” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
(2)请用“平均数法”解方程: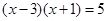 .
.
初三级一位学生对本班同学的上学方式进行了一次调查统计,图5①和图5②是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:该班共有多少名学生?
在图5①中将表示“骑车”的部分补充完整.
在扇形统计图中,“步行”部分对应的圆心角的度数是多少?
如果全年级共有300名学生,请你估算全年级骑车上学的学生人数.

如图4,△ABC中,AB=AC,D、E分别是BC、AC上的点,∠BAD与∠CDE满足什么条件时AD=AE?写出你的推理过程.
_如图3,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的△ABC是格点三角形,在建立平面直角坐标系后,点B的坐标为(-2,-2).把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形,此时点B1的坐为.
把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形,此时
点B2的坐标为.把△ABC以点A为位似中心放大为△AB3C3,使放大前后对应边长的比为1︰2,画出△AB3C3的图形.

观察下面的几个算式:
13×17=221可写成100×1×(1+1)+21;
23×27=621可写成100×2×(2+1)+21;
33×37=1221可写成100×3×(3+1)+21;
43×47=2021可写成100×4×(4+1)+21;
…… ……
根据上面规律填空:83×87可写成.
 可写成.
可写成.计算:1993×1997=.
某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?