如图，在三棱柱ABC—A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：
（1）B，C，H，G四点共面；
（2）平面EFA1∥平面BCHG.
（本题14分）已知不等式
的解集为
，
（
1）求实数
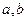的值；
（2）解关于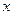
的不等式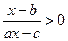
（
为实常数）
（本题12分） 若椭圆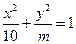
与双曲线
有相同的焦点，且椭圆与双曲线交于
点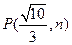
，求椭圆及双曲线的方程.
(本题12分)已知命题
；命题
表示焦点
轴上的椭圆，若
，求实数
的取值范围.
（本大题满分14分）
已知函数
，
⑴若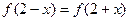
，求实数a的值？
⑵当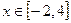
时，求函数
的最大值？
⑶当
时，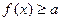
恒成立，求实
数a的最小值？
（本大题满分14分）
如图，某公园摩天轮的半径为40ｍ，圆心O距地面的高度为50ｍ，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处
（1）已知在时刻
（min）时点P距离地面的高度
，求2006min时点P距离地面的高度；
（2）当离地面（50+20
）m以上时，可以看到公园的全貌，求转一圈有多少时间可以看到公园全貌？