某商场将进货价为30元/个的台灯以40元/个的销售价售出,平均每月能售出600个.市场调研表明:当台灯的销售单价每上涨1元时,其销售量就将减少10个.
(1)若每个台灯的销售单价在40元/个的基础上涨价5元:
①涨价后,每个台灯的利润为_______元;
②涨价后,商场的台灯平均每月的销售量为_______个;
③涨价后商场平均每月销售利润___ ____元.
(2) 若设每个台灯的销售单价在40元/个的基础上涨价a元.
①试用含a的代数式填空:
涨价后,每个台灯的销售价为_______元;
涨价后,每个台灯的利润为_______元;
涨价后,商场的台灯平均每月的销售量为_______个.
②如果商场要想销售利润平均每月达到10000元,商场经理甲说“在原售价每台40元的基础上再上涨40元,可以完成任务”,商场经理乙说“不用涨那么多,在原售价每台40元的基础上再上涨10元就可以了”,试判断经理甲与乙的说法是否正确,并说明理由.
先化简,再求值 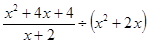 ,其中
,其中 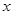 =
= 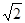
计算:
已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
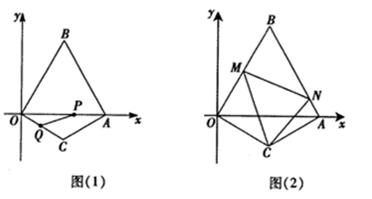
如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
已知抛物线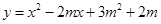
若抛物线经过原点,求m的值及顶点坐标,并判断抛物线顶点是否在第三象限的平分线所在的直线上;
是否无论m取任何实数值,抛物线顶点一定不在第四象限?说明理由;当实数m变化时,列出抛物线顶点的纵、横坐标之间的函数关系式,并求出该函数的最小函数值.
某超市经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:甲、乙两种商品的进货单价各多少元?
该超市平均每天卖出甲商品50件和乙商品20件.经调查发现,甲、乙两种商品零售单价分别每降0.2元,这两种商品每天可各多销售10件.为了使每天获取更大的利润,超市决定把甲、乙两种商品的零售单价都下降m元.设总利润为n元,请用含m的式子表示超市每天销售甲、乙两种商品获取的总利润n,在不考虑其他因素的条件下,当m定为多少时,才能使超市每天销售甲、乙两种商品获取的总利润最大?每天的最大利润是多少?