市一中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是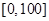 ,样本数据分组为
,样本数据分组为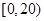 ,
,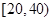 ,
,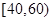 ,
,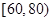 ,
,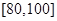 .
.
(Ⅰ)求直方图中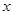 的值;
的值;
(Ⅱ)如果上学路上所需时间不少于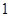 小时的学生可申请在学校住宿,若招生
小时的学生可申请在学校住宿,若招生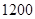 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的高一学生中任选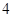 名学生,这
名学生,这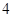 名学生中上学路上所需时间少于
名学生中上学路上所需时间少于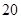 分钟的人数记为
分钟的人数记为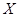 ,求
,求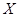 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
已知函数 .
.
(Ⅰ)设函数 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列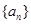 ,求证:
,求证: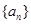 为等差数列;
为等差数列;
(Ⅱ)设函数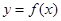 的图像的顶点到
的图像的顶点到 轴的距离构成数列
轴的距离构成数列 ,求
,求 的前
的前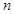 项和
项和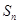 .
.
定义在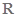 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
(1)求证: 为奇函数;
为奇函数;
(2)若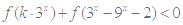 对任意
对任意 恒成立,求实数
恒成立,求实数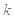 的取值范围.
的取值范围.
某医药研究所开发一种新药,据监测,如果成人按规定剂量服用该药,服药后每毫升血液中的含药量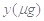 与服药后的时间
与服药后的时间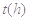 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中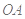 是线段,曲线段
是线段,曲线段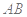 是函数
是函数
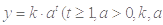 是常数
是常数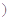 的图象.
的图象.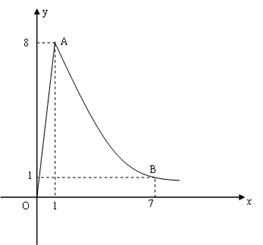
(1)写出服药后每毫升血液中含药量 关于时间
关于时间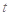 的函数关系式;
的函数关系式;
(2)据测定:每毫升血液中含药量不少于 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过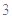
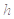 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少 ?
?
已知函数 ,且
,且 .
.
(1)求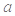 的值,并确定函数
的值,并确定函数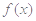 的定义域;
的定义域;
(2)用定义研究函数 在
在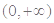 范围内的单调性;
范围内的单调性;
(3)当 时,求出函数
时,求出函数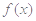 的取值范围.
的取值范围.
已知幂函数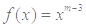 (m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足
(m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足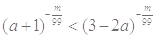 的a的取值范围.
的a的取值范围.