在学习代数式的值时，介绍了计算框图：用表示数据输入、输出框；-优题课

在学习代数式的值时，介绍了计算框图：用“”表示数据输入、输出框；用“”表示数据处理和运算框；用“”表示数据判断框（根据条件决定执行两条路径中的某一条）
（1）①如图1，当输入数x＝－2时，输出数y＝_________；
②如图2，第一个运算框“”内，应填______；第二个运算框“”内，应填______；
（2）①如图3，当输入数x＝2时，输出数y＝_____；
②如图4，当输出的值y＝37，则输入的值x ＝___________；
（3）为鼓励节约用水,决定对用水实行“阶梯价”：当每月用水量不超过15吨时（含15吨），以2元/吨的价格收费；当每月用水量超过15吨时，超过部分以3元/吨的价格收费．请设计出一个“计算框图”，使得输入数为用水量x，输出数为水费y．

科目数学题型解答题难度中等

如图所示，一次函数 $y = mx + n (m \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于第二、四象限的点 $A (- 2, a)$ 和点 $B (b, - 1)$ ，过 $A$ 点作 $x$ 轴的垂线，垂足为点 $C$ ， $ΔAOC$ 的面积为4．

（1）分别求出 $a$ 和 $b$ 的值；

（2）结合图象直接写出 $mx + n > \frac{k}{x}$ 中 $x$ 的取值范围；

（3）在 $y$ 轴上取点 $P$ ，使 $PB - PA$ 取得最大值时，求出点 $P$ 的坐标．

为了解天水市民对全市创建全国文明城市工作的满意程度，某中学数学兴趣小组在某个小区内进行了调查统计．将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．

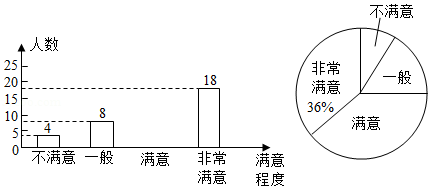
请结合图中的信息，解决下列问题：

（1）此次调查中接受调查的人数为　　人；

（2）请你补全条形统计图；

（3）扇形统计图中“满意”部分的圆心角为　　度；

（4）该兴趣小组准备从调查结果为“不满意”的4位市民中随机选择2位进行回访，已知这4位市民中有2位男性，2位女性．请用画树状图的方法求出选择回访的市民为“一男一女”的概率．

（1）计算： $4 \sin 60 ° - | \sqrt{3} - 2 | + 2020^{0} - \sqrt{12} + {(\frac{1}{4})}^{- 1}$ ．

（2）先化简，再求值： $\frac{1}{a - 1} - \frac{a - 1}{a^{2} + 2 a + 1} \div \frac{a - 1}{a + 1}$ ，其中 $a = \sqrt{3}$ ．

如图，在平面直角坐标系中，抛物线 $y = a x^{2} + bx - 2$ 交 $x$ 轴于 $A$ ， $B$ 两点，交 $y$ 轴于点 $C$ ，且 $OA = 2 OC = 8 OB$ ．点 $P$ 是第三象限内抛物线上的一动点．

（1）求此抛物线的表达式；

（2）若 $PC / / AB$ ，求点 $P$ 的坐标；

（3）连接 $AC$ ，求 $ΔPAC$ 面积的最大值及此时点 $P$ 的坐标．

如图，点 $M$ ， $N$ 分别在正方形 $ABCD$ 的边 $BC$ ， $CD$ 上，且 $∠ MAN = 45 °$ ．把 $ΔADN$ 绕点 $A$ 顺时针旋转 $90 °$ 得到 $ΔABE$ ．

（1）求证： $ΔAEM ≅ ΔANM$ ．

（2）若 $BM = 3$ ， $DN = 2$ ，求正方形 $ABCD$ 的边长．