如图所示,一次函数的图象与反比例函数的图象交于第二、四象限的点和点,过点作轴的垂线,垂足为点,的面积为4.
(1)分别求出和的值;
(2)结合图象直接写出中的取值范围;
(3)在轴上取点,使取得最大值时,求出点的坐标.

(本题满分8分,每小题各4分)(1)解方程:

(2)计算:

如图,对称轴为直线 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).⑴求抛物线解析式及顶点坐标;
⑵设点E(x,y)是抛物线第四象限上一动点,四边形OEAF是以OA为对角线的平行四边形,求
 OEAF的面积S与x之间的函数关
OEAF的面积S与x之间的函数关 系式,并求出自变量的取值范围;
系式,并求出自变量的取值范围;⑶若S=24,试判断
 OEAF是否为菱形。
OEAF是否为菱形。⑷若点E在⑴中的抛物线上,点F在对称轴上,以O、E、A、F为顶点的四边形能否为平行四边形,
 若能,求出点E、F的坐标;若不能,请说明理由。(第⑷问不写解答过程,只写结论)
若能,求出点E、F的坐标;若不能,请说明理由。(第⑷问不写解答过程,只写结论)
某学校规定,该学校教师的每人每月用电量不超过A度,那么这个月只需交10 元电费,如果超过A度,则这个月除了仍要交10元用电费外,超过部分还要按每度
元电费,如果超过A度,则这个月除了仍要交10元用电费外,超过部分还要按每度 元交费.
元交费.⑴胡教师12月份用电90度,超过了规定的A度,则超过的部分应交电费多少元?(用含A的代数式表示)
⑵下面是该教师10月、11月的用电情况和交费情况:
| 月份 |
用电量(度) |
交电费总额(元) |
| 10月份 |
45 |
10 |
| 11月份 |
80 |
25 |
根据上表数据,求A 值,并计算该教师12月份应交电费多少元?
值,并计算该教师12月份应交电费多少元?
如图以O为圆心的两个同心圆,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B,小圆的切线AC与大圆相交于点D,且OC平分∠ACB.⑴试判断BC所在的直线与小圆的位置关系,并说明理由;
⑵试判断线段AC、AD、BC之间的数量关系,并说明理由;
⑶若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积(结果保留π).

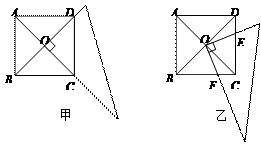
将一块三角板的直角顶点放在正方形ABCD的对角线交点位置,两边与对角线重合如图甲,将这块三角板绕直角顶点顺时针方向旋转(旋转角小于90°)如图乙.⑴试判断△ODE和△OCF是否全等,并证明你的结论.
⑵若正方形ABCD的对角线长为10,试求三角板和正方形重合部分的面积.