已知，平面直角坐标系中，矩形OABC的边OC在x轴正半轴上，边OA在y轴正半轴上，B点的坐标为（4，3）．将△AOC沿对角线AC所在的直线翻折，得到△AO’C，点O’为点O的对称点，CO’与AB相交于点E（如图①）．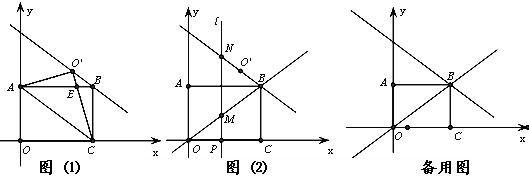

（1）试说明：EA＝EC；
（2）求直线BO’的解析式；
（3）作直线OB（如图②），直线l平行于y轴，分别交x轴、直线OB、O’B于点P、M、N，设P点的横坐标为m （m>0）。y轴上是否存在点F，使得ΔFMN为等腰直角三角形？若存在，请求出此时m的值；若不存在，请说明理由.

科目 数学   题型 解答题   难度 中等

知识点： 一次函数的最值