甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满8局时停止.设甲在每局中获胜的概率为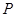 (
(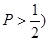 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为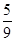 .
.
(1)求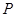 的值;
的值;
(2)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
在四边形ABCD中,AD⊥CD,AD=5,AB=7,∠BDA=60º,∠CBD=15º,求BC长.
已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
在直角坐标系xOy中,直线l的参数方程为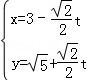 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为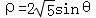 .
.
(Ⅰ)求圆C的圆心到直线l的距离;
(Ⅱ)设圆C与直线l交于点A、B.若点P的坐标为(3,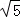 ),求|PA|+|PB|.
),求|PA|+|PB|.
如图,已知AB圆O的直径,C、D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.
(Ⅰ)求证:C是劣弧BD的中点;
(Ⅱ)求证:BF=FG.
已知函数f(x)=x2﹣alnx,a∈R.
(Ⅰ)当a=4时,求函数f(x)在[1,e]上的最小值及相应的x的值;
(Ⅱ)若存在x∈[2,e],使得f(x)≥(a﹣2)x成立,求实数a的取值范围.