（本小题满分12分）设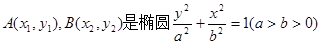
上的两点，已知
，
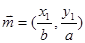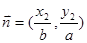，若
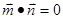且椭圆的离心率
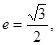短轴长为2，
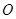为坐标原点.
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；（Ⅲ）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由
已知命题
：方程
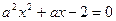在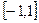
上有且仅有一解；命题
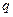：只有一个实数
满足不等式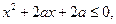
若命题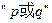
是假命题，求
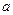的取值范围.
已知函数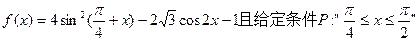
。
（Ⅰ）求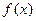
的最大值及最小值；
（Ⅱ）若又给条件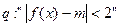
且
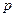是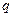
的充分条件，求实数
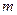的取值范围。
已知
：
，
：
且是的必要不充分条件，求实数
的取值范围。
分别指出由下列各组命题构成的逻辑关联词“或”、“且”、“非”的真假。
（1）p: 梯形有一组对边平行；q：梯形有一组对边相等。
（2）p: 1是方程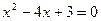
的解；q：3是方程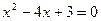的解。
（3）p: 不等式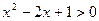
解集为R；q: 不等式
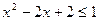解集为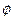
。
（4）p: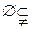 
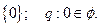
判断下列语句是不是命题，如果k，，，是，说明是全称命题还是特称命题.
(1) 中国的所有江河都流入太平洋；
(2) 
不能作除数；
(3) 有一个实数
，不能取对数；
(4)每一个向量都有方向吗？