某科技开发公司研制出一种新型产品,每件产品的成本为2400 元,销售单价定为3000 元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000 元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10 元,但销售单价均不低于2600 元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600 元?
(2)设商家一次购买这种产品x 件,开发公司所获的利润为y 元,求y(元)与x(件)之间的函数关系式,并写出自变量x 的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.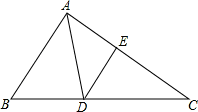
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
一不透明的袋子中装有4个球,它们除了上面分别标有的号码l、2、3、4不同外,其余均相同。将小球搅匀,并从袋中任意取出一球后放回;再将小球搅匀,并从袋中再任意取出一球。求第二次取出球的号码比第一次的大的概率。(请用“画树状图”或“列表”的方法给出分析过程,并写出结果)
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
| 1号 |
2号 |
3号 |
4号 |
5号 |
总数 |
|
| 甲班 |
89 |
100 |
96 |
118 |
97 |
500 |
| 乙班 |
100 |
95 |
110 |
91 |
104 |
500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)求两班比赛成绩的中位数.
(3)比较两班比赛数据的方差哪一个小.
(4)根据以上三条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,此时点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
解下列方程:
(1)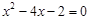
(2)8(3 -x)2 –72=0