小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤，在纸上逐步探索函数y2=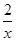
的图象，并且在黑板上写出4个点的坐标：A（
，
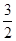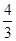），B（1，2），C（1，
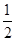），D（﹣2，﹣1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y1=x+1又在双曲线y2=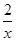上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y2=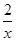上的概率．
（1）解方程：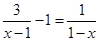
（2）解不等式组：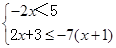
．
化简：
（1）
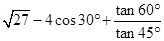
（2）
．
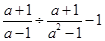如图，在平面直角坐标系xOy中，矩形OEFG的顶点E坐标为（4，0），顶点G坐标为（0，2）．将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．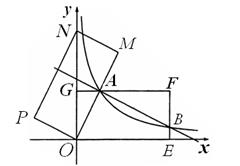
（1）判断△OGA和△NPO是否相似，并说明理由；
（2）求过点A的反比例函数解析式；
（3）若（2）中求出的反比例函数的图象与EF交于B点，请探索：直线AB与OM是否垂直，并说明理由．
（本题10分）我校八年级举行英语风采演讲比赛，派两位老师去超市购买笔记本作为奖品．据了解，该超市的甲、乙两种笔记本的价格分别是10元和6元，他们准备购买这两种笔记本共30本．
（1）若这两位老师计划用220元购买奖品，则能买这两种笔记本各多少本?
（2） 若他们根据演讲比赛的设奖情况，决定所购买的甲种笔记本的数量不多于乙种笔记本数量的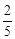
，但又多于乙种笔记本数量的
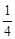，若设他们买甲种笔记本x本，买这两种笔记本共花费y元．
①求出y（元）关于x（本）的函数关系式；
②问购买这两种笔记本各多少时，花费最少，此时的花费是多少元？
-1，求a2+2a-1的值.