在直角坐标 中,圆
中,圆 ,圆
,圆 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆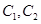 的极坐标方程,并求出圆
的极坐标方程,并求出圆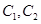 的交点极坐标(用极坐标表示);
的交点极坐标(用极坐标表示);
(Ⅱ)求圆 的公共弦的参数方程。
的公共弦的参数方程。
某城市理论预测2007年到2011年人口总数与年份的关系如下表所示
| 年份2007+x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数y(十万) |
5 |
7 |
8 |
11 |
19 |
(1)请根据上表提供的数据,求最小二乘法求出Y关于x的线性回归方程;
(2)据此估计2016年该城市人口总数。
学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;
单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
| 损坏餐椅数 |
未损坏餐椅数 |
总 计 |
|
| 学习雷锋精神前 |
50 |
150 |
200 |
| 学习雷锋精神后 |
30 |
170 |
200 |
| 总计 |
80 |
320 |
400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
有人要走上一个楼梯,每步可向上走一级台阶或二级台阶,我们用 表示该人走到
表示该人走到 级台阶时所有可能不同走法的种数,试寻求
级台阶时所有可能不同走法的种数,试寻求 的递推关系。
的递推关系。
(本小题满分12分)已知 .
.
(1)是否存在常数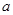 、
、 ,使得
,使得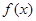 的值域为
的值域为 ?若存在,求出
?若存在,求出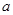 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(2)在(1)的条件下,求函数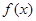 的单调区间.
的单调区间.