.已知圆 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.
(1)若直线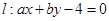 平分圆
平分圆 的周长,求原点O到直线
的周长,求原点O到直线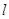 的距离的最大值;
的距离的最大值;
(2)若圆 平分圆
平分圆 的周长,圆心
的周长,圆心 在直线y=2x上,求符合条件且半径最小的圆B的方程.
在直线y=2x上,求符合条件且半径最小的圆B的方程.
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| 关注NBA |
不关注NBA |
合计 |
|
| 男生 |
6 |
||
| 女生 |
10 |
||
| 合计 |
48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?
⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望。
附: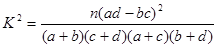 ,其中
,其中 
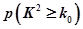 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
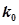 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
函数 ,其中
,其中 为常数,且函数
为常数,且函数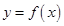 和
和 的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。
的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。
为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的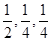 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求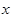 的分布列及期望。
的分布列及期望。
已知函数 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
设 ,且
,且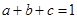 ,证明不等式:
,证明不等式: